本帖最后由 gtj05 于 2011-5-21 15:28 编辑
2 D6 V. K7 T4 Y. H# q+ W# I4 g) G2 f% j: _
内容介绍:
% m7 s0 S. h/ l9 @* E7 w3 U6 S7 S1.你将从本资料中学到,一个设计是否功能良好和公差合理,零部件是否能被组装相对比较容易预测。要知道零部件在组装中,由于公差而引起的位移产生的间隙大小或干涉情况,就需要懂得尺寸链公差叠加计算知识。实现避免公差过小产生浪费,避免公差过大影响产品功能。
. I, H# S: j: x, [4 x% p/ B
0 r) A& j8 B7 E5 d% i+ X6 W4 | 2. 讲解如何建立公差和进行两维公差设计分析,使用大量问题案例,进行几何尺寸链公差叠加计算训练。你将学会如何研究零部件公差累积,帮助应用GD&T提升设计水平、产品稳健性,优化质量成本周期,从而达到满足产品功能要求,且减少产品成本。实现产品功能和成本最经济的应用方法. 目录 第一章:尺寸链公差叠加介绍 (TSU Introduction) - 什么是尺寸链公差叠加?(What’s TSU?)
- 尺寸链公差叠加能解决什么问题?(What issues TSU can solve?)
- 尺寸链公差叠加的作用(Function of TSU)
- 尺寸链公差叠加的类型(Categories of TSU)
第二章:线性尺寸链公差叠加(Linear TSU) - 线性尺寸链公差叠加步骤(TSU calculation steps)
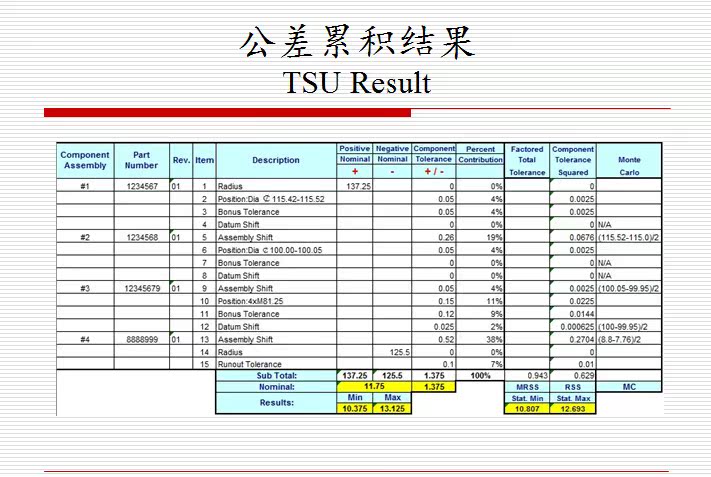
- 线性尺寸链公差叠加计算总结(TSU Summary)
- 线性尺寸链公差叠加计算练习(TSU Exercises)
第三章:零件位置度尺寸链公差叠加(Part TSU Using Position) - 位置度尺寸链公差输入(Entry of Positional Tolerance)
- 位置度尺寸链公差叠加(Positional TSU)
- 位置度尺寸链公差叠加带基准偏移(Positional TSU With Datum Shift)
- 位置度公差叠加示例(Example of Positional TSU)
- 复合位置度公差叠加(Composite Positional TSU)
- 位置度公差叠加练习(Positional TSU Exercises)
第四章:装配件位置度尺寸链公差叠加(Assembly TSU Using Position) - 位置度尺寸链公差叠加,RFS(Positional TSU of Assembly, RFS)
- 位置度尺寸链公差叠加,MMS(Positional TSU of Assembly, MMS)
- 位置度尺寸链公差叠加有基准偏移(Positional TSU of Assembly with DatumShift)
第五章:轮廓度尺寸链公差叠加(TSU Using Profile Controls) - 轮廓度理论尺寸和公差的输入(Dimension and Tolerance Entry of Profile)
- 零件轮廓度尺寸链公差叠加(Profile TSU of Parts)
- 复合轮廓度尺寸链公差叠加(Composite Profile TSU of Parts)
; W. K8 I) N5 } ]0 G# W7 ?3 B4 m# Z' D2 z+ D/ y x/ N
第六章:形状度尺寸链公差叠加(TSU Using Form) - 形状度尺寸链公差叠加(Form tolerance stack-up)
- 平面度尺寸链公差叠加(Flatness TSU)
- 平面度尺寸链公差叠加示例(Example of Flatness TSU)
; B, m. H/ g) |" T9 O) N: G; i& D) Y4 b# B
第七章:方向度尺寸链公差叠加(TSU Using Orientation) - 方向度尺寸链公差叠加介绍(Orientation TSU Introduction)
- 垂直度尺寸链公差叠加(TSU Using Perpendicularity)
- 垂直度尺寸链公差叠加FOS(TSU Using Perpendicularity, FOS)
第八章:跳动度尺寸链公差叠加(TSU Using Runout) - 零件跳动度尺寸链公差叠加(Runout TSU)
- 零件跳动度尺寸链公差叠加练习(Part Runout TSU Exercise)
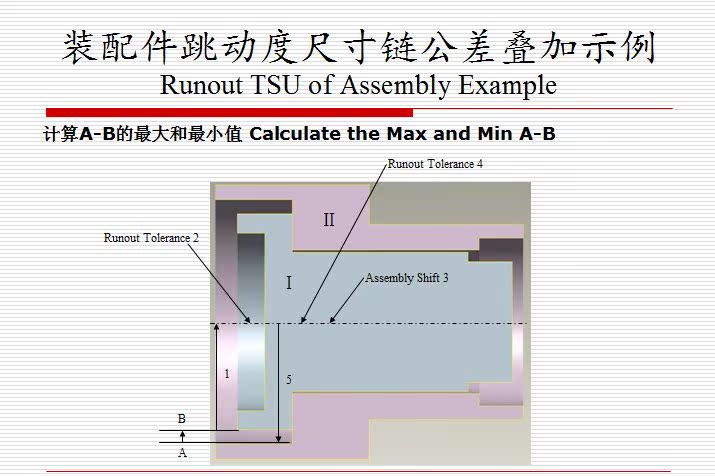
- 装配件跳动度尺寸链公差叠加(Runout TSU of Assembly)
- 装配件跳动度尺寸链公差叠加示例(Assembly Runout TSU Example)
- 装配件跳动度尺寸链公差叠加练习(Assembly Runout TSU Exercise)
第九章:综合尺寸链公差叠加(TSU Using Multiple Geometric Control - 示例1 Example 1
- 示例2 Example 2
- 示例3 Example 3
) V# d0 K( U2 X- R需要的发本人QQ邮箱^^^
$ |1 m" S4 i% h: r5 P
, b& l" y& ^. C* W8 Y+ G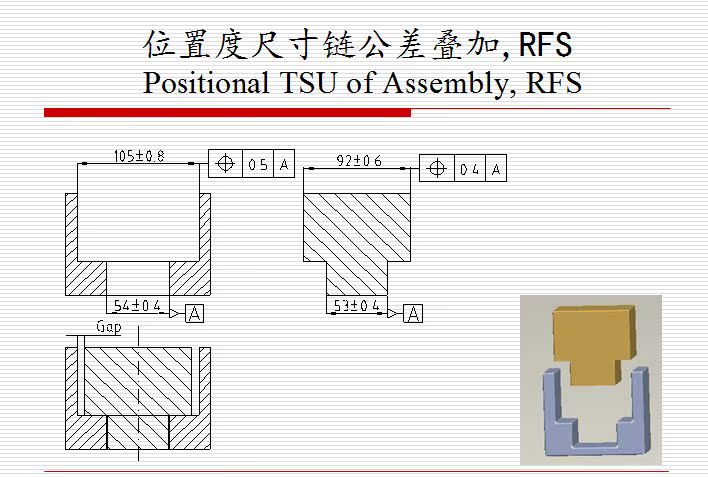 2 M% F! l3 y( d9 V 2 M% F! l3 y( d9 V
/ F0 W( J$ [- Y- Q5 U$ C6 |) F: Q* |6 j9 R# f
 ( C8 s3 |' u }! n$ Y ( C8 s3 |' u }! n$ Y
Z! k- M( a) ?# O, o
+ E3 R2 X) V5 }* J' Z k( o* f# F _" k3 n
* @. r" ? J5 {/ F( B! V. y
# R! t" p! B& m; ?
3 N. t: k- q( y D' k y1 L4 M. U
; w5 Z, w1 h8 }1 G- _% y) r0 ^) O `
 . \& F F6 ]( S V% z . \& F F6 ]( S V% z
; e/ \1 D9 C& `* F5 i- A" O
* k' I% v7 ^/ N
. T f4 `+ ]9 t0 f/ L6 n8 ?9 e0 o" _' t/ @( A3 r8 p4 D1 i' \
8 d' T0 }8 D4 a8 I
/ z! K3 o: n3 X& _ g. g
 尺寸链公差叠加分析.part1.rar
(957.03 KB, 下载次数: 761)
6 X" n% j2 z" o5 R
尺寸链公差叠加分析.part1.rar
(957.03 KB, 下载次数: 761)
6 X" n% j2 z" o5 R
; k0 l! y; F! C* {" q
: ]/ a& z9 X9 [& g* G! c
 尺寸链公差叠加分析.part2.rar
(866.63 KB, 下载次数: 726)
尺寸链公差叠加分析.part2.rar
(866.63 KB, 下载次数: 726)
| 
 |关于我们|sitemap|小黑屋|Archiver|手机版|UG网-UG技术论坛-青华数控模具培训学校
( 粤ICP备15108561号 )
|关于我们|sitemap|小黑屋|Archiver|手机版|UG网-UG技术论坛-青华数控模具培训学校
( 粤ICP备15108561号 )